云计算 计算机

Paxos算法

Posted by jkofbr on November 28, 2025

正文

系统中角色

Proposer

  • 发起提案

    Acceptor

  • 参与决策，回应Proposer提案

    Learner

  • 不参与决策，仅学习最新达成一致的提案

    算法流程

    Prepare阶段

    Prepare & Promise

  • Proposer
    • 生成全局唯一、递增的Proposal ID(一般用时间戳+Server ID)
    • 向所有Accepter发送==仅包含Proposal ID==的Prepare请求。
  • Acceptors
    • 在收到Prepare请求后进行Promise承诺

      Promise

  • 两个承诺
    1. 不再接受==Proposal ID <= 当前请求==的Prepare请求
    2. 不再接受==Proposal ID < 当前请求==的Proposal请求
  • 一个应答
    1. 在不违背前述承诺的情况下，回复已经Accept的提案中Proposal ID最大的那个提案的Value和Proposal ID(==使Proposer达成一致==)

      Accept阶段

      Proposal & Accept

  • Proposer
    • 在收到==多数==Acceptor的Promise后，向所有的Acceptor发出Proposal请求
  • Acceptor
    • 在收到Proposal请求后进行Accept处理

      Learn阶段

  • Proposer
    • 在收到==多数==Accept后(标志着决议通过)，向Learner发送决议结果
  • Learner
    • 学习决议结果

      伪代码

      600

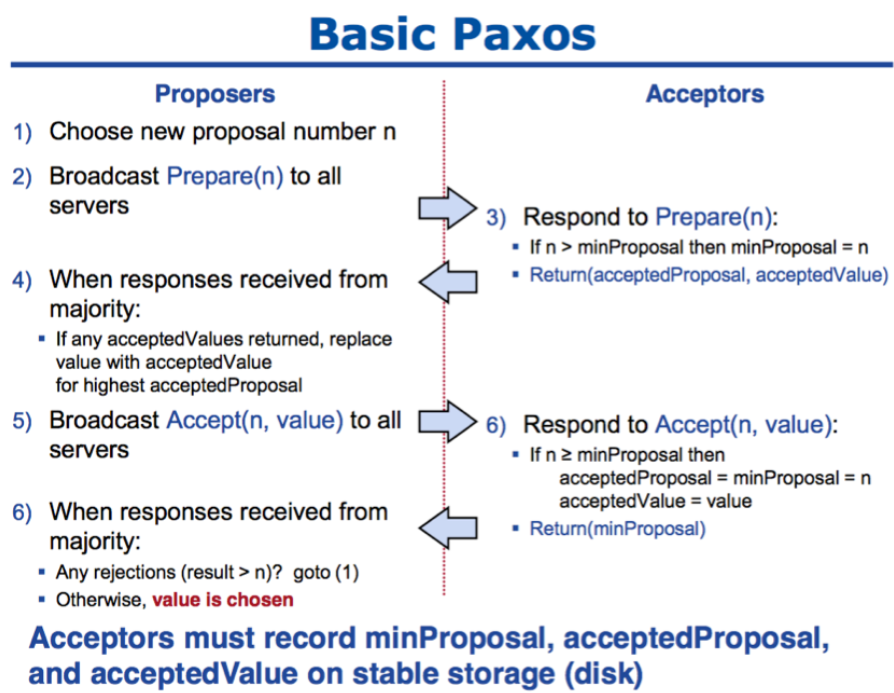
      示例

  • 注意：$S_1$和$S_5$是proposer，其他是Acceptor
  • P代表Prepare阶段，A代表Accept阶段
  • 3.1和4.5是Proposal ID(3.1 ：3为时间戳，1为Server ID)
  • 示例1
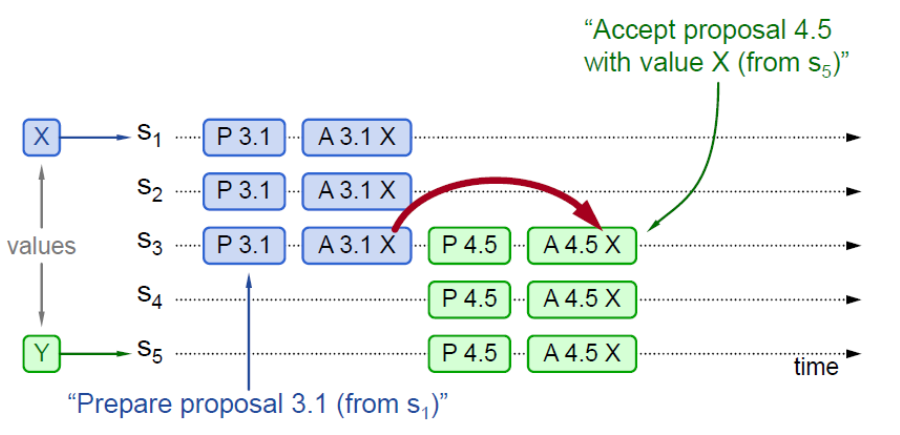
    • $S_3$在收到$S_5$的Prepare请求后返回了——已经Accept的提案中Proposal ID最大的那个提案的Value和Proposal ID(详见一个应答)
    • $S_5$在收到过半数回复后，发现有来自$S_3$的acceptedValue返回，因此找寻所有回复中acceptedProposal最大的(即来自$S_3$的4.5)，将其所对应的acceptedValue(即来自$S_3$的Y)作为本次提案的value(==使Proposer达成一致==)
    • 后续该Proposal被Accept，所有节点达成一致
  • 示例2
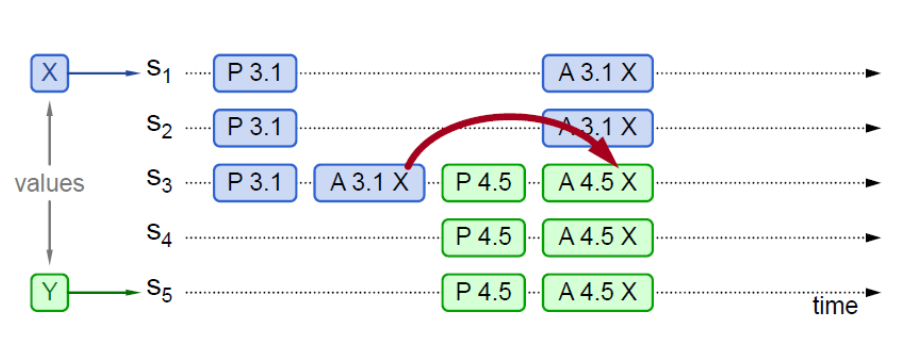
    • 过程类似示例1
  • 示例3
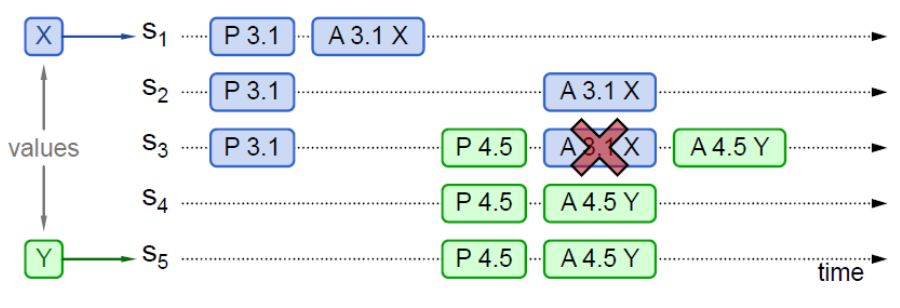
    • $S_3$在接受[A 3.1 X]前就已经收到[P 4.5]，因此并未通过该Proposal(详见两个承诺)
  • 示例4(活锁)
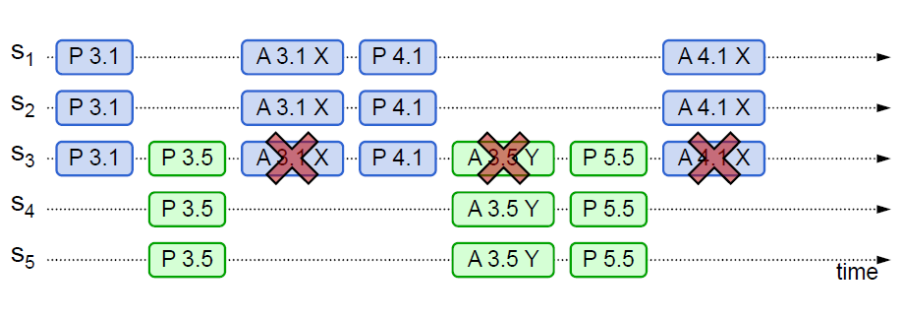
    • 两个Proposer交替在另一位Accept成功前Prepare成功，形成活锁(Livelock)
    • 可以通过随机数来决定proposer重新发送Prepare请求的间隔时间

      理论推导过程

      前提：若只有一个Proposer提出了一个value，那么这个value必须被最终选定。

由此推导出约束1

[!highlight] P1：一个Acceptor必须接受它收到的第一个提案。

这又造成另外的问题

  • 每个Proposal分别提出不同的Value，不同的Acceptor接受到了这些不同的Value，则会导致不同的value被选定 为了避免该问题，需要添加一个规定
  • ==规定：一个提案被选定需要被半数以上的Acceptor接受== 但这个规定又要求每个Acceptor必须能够接受不止一个提案，否则将导致没有Proposal被Accept(每个Proposal只被少于半数的Acceptor通过) 此时一个Proposal仅包含Value已经不足以让Acceptor做出唯一的判断了，因此需要加入其他信息
  • Proposal=Value —> Proposal = (n, Value)
  • 通过编号n的大小来选择 此时已经可以保证多个Proposal的选择了，但是仍需保证所有被选择Proposal具有相同的Value，否则又会出现不一致的情况

因此提出约束2

[!highlight] P2：如果某个value为v的提案被选定了，那么每个编号更高的被选定提案的value必须也是v。

为了落实该约束，提出约束Acceptor的约束P2a

[!highlight] P2a：如果某个value为v的提案被选定了，那么每个编号更高的被Acceptor接受的提案的value必须也是v。

为了实现P2a又需要对Proposer做出规定P2b，否则若有多个Proposer持有不同’Value的情况下，仅会有第一个Proposal被接受，其他的Proposer的proposal则一直无法通过，导致其无法与大家同步

[!highlight] P2b：如果某个value为v的提案被选定了，那么之后任何Proposer提出的编号更高的提案的value必须也是v。

为了实现P2b，仅需满足P2c和P1a即可

[!highlight] P2c：对于任意的N和V，如果提案[N, V]被提出，那么存在一个半数以上的Acceptor组成的集合S，满足以下两个条件中的任意一个：

  • S中每个Acceptor都没有接受过编号小于N的提案。
    • 若S中每个Acceptor都接受了编号大于N的提案
      • 则P2b成立，因为该提案[N, V]不会被选定
  • S中Acceptor接受过的最大编号的提案的value为V。

    [!highlight] P1a：Acceptor可以接受（Accept）编号为n的Proposal当且仅当它没有回复过一个具有更大编号的Prepare消息。

  • 易看出P1a同时也能推出P1
  • 因此P2c和P1a是理论的基础
CATALOG
    FEATURED TAGS
    FRIENDS